C’est quoi une forme d’onde et comment ça fonctionne ?

Une forme d’onde est une représentation graphique d’une onde.

La synthèse sonore repose sur 5 formes d’onde. Le sinus, le triangle, la dent de scie, la pulsation (qui n’est pas abordé dans cet article), et le carré (qui est un cas particulier de la pulsation).

👉 Une forme d’onde est un graphique qui affiche les changements d’amplitude, ou de niveau au fil du temps.

L’amplitude est mesurée de manière bipolaire, avec des valeurs positives (+) et négatives (-).

À ne pas confondre avec level, qui peut être la valeur absolue des changements d’amplitude, ou une moyenne.

➡️ Les formes d’onde contiennent généralement des dizaines de milliers de changements discrets, dans une période extrêmement courte, entassés dans un bloc dans un séquenceur.

👀 Quand on zoom sur une forme d’onde, son contour devient de plus en plus visible.

 

À quoi ça sert de connaître les formes d’onde de base ?

Apprendre les formes d’onde de base dans la synthèse sonore vous aidera à :

• exploiter les capacités des synthétiseurs modernes,
• obtenir le timbre souhaité même pendant les performances en live,
• comprendre le comportement des oscillateurs (VCO, oscillateur commandé en tension) et des modulateurs (LFO, oscillateur basse fréquence),
• utiliser ces formes d’onde dans des dérivations mathématiques d’analyse, de synthèse et d’effets audio,
• écrire du code pour générer ces formes d’onde, pour les algorithmes de synthèse sonore et d’effets audio,
• détecter toute incohérence de ces signaux dans un système,
• éviter les problèmes potentiels de crénelage (le crénelage est l’effet du chevauchement des composants de fréquence résultant d’une fréquence d’échantillonnage insuffisamment élevée. Cela provoque l’apparition de fréquences dans le spectre amplitude-fréquence, qui ne sont pas dans le signal d’origine),
• découvrir d’où le repliement peut provenir.

 

PCM & Fréquence de Nyquist

 

👉 Une forme d’onde est une recréation numérisée de changements de tension, très dynamiques au fil du temps.

Les changements discrets d’un signal d’entrée sont rectifiés en un court instant, grâce au processus Pulse Code Modulation (PCM).

Le PCM attribue une valeur de bit à chaque échantillon, à la fréquence d’échantillonnage.

💻 Plus la profondeur de bits est élevée, plus l’ordinateur doit choisir de valeurs, et plus la rectification est précise.

Le taux d’échantillonnage pour enregistrer est assez standard. 44100 Hz, la  fréquence de Nyquist pour l’audio.

👂 La fréquence audible la plus élevée pour l’homme est de 20 000 Hz.

Chaque fréquence a une moitié positive et une moitié négative (compression & raréfaction).

➡️ Tant que l’échantillonnage est réalisé suffisamment rapidement afin de capter, à la fois les parties positives et négatives de la fréquence audible la plus élevée (oscillant le plus rapidement), il est possible de rectifier presque toutes les fréquences audibles.

Cela veut dire qu’à une fréquence d’échantillonnage de 40 000 Hz, nous capterons à la fois les parties positives et négatives à 20 000 Hz.

👉 Cependant, comme les ondes sinusoïdales sont infiniment lisses et graduelles, un seul échantillon de chaque portion ne produira pas une forme d’onde très précise, à des fréquences très élevées et très basses.

C’est la raison pour laquelle les 4100 Hz supplémentaires dans la fréquence de Nyquist existent.

Il tient compte de tout crénelage qui peut se produire lors de l’échantillonnage de très basses, et très hautes fréquences.

 

Pourquoi ne pas échantillonner aussi souvent que possible ?

Pourquoi ne pas simplement passer à 50 000 Hz ou 100 000 Hz ?

➡️ La réponse est la négligence.

Nous ne pouvons pas entendre l’amélioration au-delà de 44100 Hz. Mais ça ne veut pas dire que d’autres taux d’échantillonnages ne sont pas utilisés !

Par exemple, lors de la production de son, la fréquence d’échantillonnage de l’audio doit correspondre à la fréquence de résolution vidéo, qui est souvent supérieure à 90 000 Hz.

 

Formes d’ondes synthétiques

👉 Les formes d’onde synthétiques sont beaucoup moins complexes que l’audio enregistré, à partir d’une source acoustique ou électrique.

Ils permettent de créer des sons à partir de zéro.

Ce sont les 4 formes d’onde synthétiques.

 

Sinus

Le sinus est la plus basique des formes d’onde de synthèse sonore.

La formule du sinus :$$(t)=\sin (2\pi ft),(1)$$

où f est la fréquence de la sinusoïde en Hz, et t est le temps en secondes

Même les oscillateurs et les filtres auto-résonnants les plus purs, ont un peu de bruit dans leur sortie.

Y = Asinx le décrit mathématiquement.

 

 

Carré

👉 L’onde carrée est plus intéressante que la sinusoïdale ou le triangle, en raison de son timbre vide caractéristique.

où f est la fréquence du carré en Hz, et t est le temps en secondes.

Elle contient des harmoniques impaires (multiples entiers impairs de la fondamentale).

Cela signifie que si la fréquence fondamentale d’une onde carrée est de 200 Hz, elle générera également 600 Hz (3ème harmonique), 1000 Hz (5ème harmonique), 1400 Hz (7ème harmonique) etc.

 

 

Triangle

La formule du triangle est :

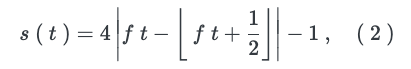
où f est la fréquence du triangle en Hz, et t est le temps en secondes.

👉 La forme d’onde en triangle est comme une onde carrée, en ce qu’elle contient des harmoniques impaires, à l’exception du contenu harmonique, dont l’amplitude est inférieure à celle d’une onde carrée.

Cela signifie que les harmoniques ont moins d’influence sur la forme globale de l’onde.

 

 

Dent de scie

👉 Cette forme d’onde contient toutes les harmoniques.

C’est la plus complexe des 4 formes d’onde synthétiques de base (mais loin d’être aussi complexe que le son réel).

Le spectre de la forme d’onde en dents de scie contient des harmoniques paires et impaires.

La fréquence fondamentale d’une dent de scie est de 100 Hz, cela signifie qu’elle contient aussi 200 Hz, 300 Hz, 400 Hz etc.

Chaque harmonique est un peu plus faible en amplitude par rapport à la précédente.

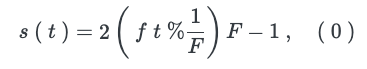
où f est la fréquence de la dent de scie en Hz, t le temps en secondes, et % est l’opérateur modulo appliqué aux valeurs réelles.

 

 

Petite conclusion

Les ondes triangulaires, carrées et en dents de scie sont composées d’ondes sinusoïdales.

Essentiellement, on peut synthétiser une onde carrée assez précise en ajoutant des multiples impairs, de la fréquence fondamentale à une onde sinusoïdale.